（毎週火・木・土曜日は、パートナーエッセイにお付き合いください。）

皆さんこんにちは、パートナーの石野雄一です。

いままでは会計の話でしたが今回から、だんだんとファイナンスっぽくなっていきます。

まずは、「単利」と「複利」の違いについて復習です。

あなたが、いま100万円持っているとします。

この100万円を年率10％の定期預金で、
５年間運用するとします。

１年後には口座残高は110万円になります。

元本100万円に１年間で利息が、
10万円（＝100万円×10％）ついたわけです。
このときの利息額は、
元本100万円に利率10％をかけて計算することができます。

ところが、
あなたは、せっかくついた利息10万円を、
預金口座から引き出してしまいます。
預金残高は当然のことながら、
100万円になります。

２年目もまた１年目と同じように10万円の利息がつき、
２年後には、口座残高は110万円になります。

ここでもまた、あなたは利息の10万円を引き出すとします。
いつまでたっても、あなたの預金口座は100万円のままです。

あなたが５年間で、
引き出した利息額を合計すると50万円になります。
これって、あたりまえです。

元金と利息を合わせて考えれば、
お金は５年間で100万円から150万円に増えたことになります。

このように利息を現金で引き出してしまって、
利息そのものを運用しない方法を「単利」といいます。

それでは、「複利」の場合はどうでしょうか？

複利の場合は、
いっさい預金口座からお金を引き出さないようにします。
つまり、１年後に110万円（元金100万円＋利息10万円）になったら、
そのままにしておくわけです。
こうすれば、
２年後には110万円に対して10％の利息がつきますから、
口座残高は121万円になっているわけです。

３年後には、さらにこの121万円に10％の利息がつきますから、
133万円になります。

５年後の口座残高は、約161万円となっています。

利息を毎年引き出していると、お金は150万円にしかなりませんでした。

ところが利息をそのままにしておけば、その利息に対して利息がつきますから、５年後の口座残高は161万円になるわけです。

「利息が利息を生む」というのが複利の特徴です。

その複利効果で、
単利の時よりも約11万円ものお金が増えたわけです。

ファイナンスで、
これから出てくる利息計算は、
全て、「複利」が前提になっていることを覚えておいてください。

複利の計算で、中学校以来、
久しぶりに数式に触れた人もいるかも知れません。
次に、将来価値について説明しましょう。
将来価値といっても、そんなに難しいことではありません。

将来価値とは、
今のお金を複利で運用した場合に、
将来どのような価値になるのかということです。
つまり、現在のある価格（＝価値）の、
将来における価値っていうことです。
そのまんまの意味です（笑）

ここで問題です。
今の100万円を金利10％で１年間運用した場合、
将来価値はいくらになるでしょうか？

これは、次のように求めることができます。

100万円×（１＋10％）＝110万円

（1＋10％）を掛けることの意味がわからないっていうあなたは、
次のように分解してみましょう。

100万円×（１＋10％）＝100万円×1＋100万円×10％＝110万円

こう考えると最初の「1」は、
元本のためにあるがわかるでしょう。
この「１」がないと利息額10万円だけが、
計算されるということになってしまいます。

どんどん行きましょう。
２年目は、この110万円に対して、
また同じように、（１＋10％）をかけます。

110万円 ×（１＋10％）＝121万円

現在の100万円の３年後における将来価値を求める場合は、
次のように計算すれば、133万円であることがわかります。
100万円×（１＋10％）＝110万円
110万円×（１＋10％）＝121万円
121万円×（１＋10％）＝133万円
また、次のように表現することもできます。

100万円×（１＋10％）×（１＋10％）×（１＋10％）
＝100万円×（１＋10％）＾3＝133万円

最初のお金100万円を年率10％で3年間運用するわけですから、
（１＋10％）を３回かけるわけです。

（このように同じものを複数回掛け合わせることを「べき乗」といいます）
この計算からもわかるように、現在のX円のｎ年後の将来価値（FV：Future Value）は、次のように計算することができます。

将来価値 = X ×（1+金利）＾n

ちなみに、
EXCELで「べき乗」を計算するときに使う記号「＾」は、
キャレットっていうんですよ。

って、関係ないですね。

次は、中級編です。

通常、金融機関の商品は、
１年に１回だけ利息がつくのではありません。
むしろ、半年毎に利息がつくということも珍しくありません。
たとえば、「年利５％で半年複利」といえば、
半年で、利率2.5％の利息がつくということです。

つまり、半年たったところで、
半年分の利息を元本に加えて、
次の半年の金利を計算するということです。

100万円を「年利５％で半年複利」で運用してみましょう。

まず、半年たったときには、
100万円×（1+2.5%）=102.50万円
となります。

次の半年では、
この102.50万円に利息がつきますから、
102.50万円×（1+2.5%）=105.0625万円
となります。

つまり、100万円を「年利5％で半年複利」で運用すると、
一年後には、
100万円×（1+2.5%）^2=105.0625万円
となるわけです。

この計算からもわかるように、
現在のX円は、年率ｒ％、年ｍ回利息受取の
複利で運用した場合、ｔ年後の将来価値は、
次のように計算できます。

このように、
たとえ同じ期間、同じ年率で、運用したとしても、
利息がつく回数が増えれば増えるほど、
将来価値は大きくなるのです。

ここからは、上級編です。
イヤな予感がする人は、読み飛ばしてください。

さきほど、利息がつく回数が増えれば増えるほど、
将来価値が大きくなるといいました。

それでは、
利息のつく回数がとっても多くなると
どうなるのでしょうか？

つまり、
 の  が無限大に近づくということです。

を無限大に近づけると、

 は  に近づいていく

ということがわかっています。

ちなみに は「自然対数の底」と呼ばれ、
2.71828182845904という数字です。

このように連続的に利払いを行う利息の計算方法を
連続複利といいます。

したがって、現在のX円は、
年率ｒ％、連続複利で運用した場合、ｔ年後の将来価値
は、次のように計算することができます。

なんで、こんなに難しいことやるんだろう？
と思いますよねぇ。
でも、この連続複利という考え方は、
金融工学では必須ですので、
頭の片隅に置いておいてください。

実際に連続複利を計算する場合は、
それほど、難しくはありません。
EXCELには、EXPという関数があるからです。

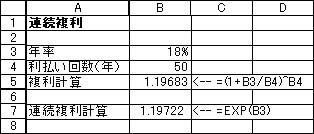
1円を年利18％で運用した場合（年50回利払い）、
1年後の将来価値は、次のように計算できます。

一方、連続複利で計算すると、
 になります。

もちろん、
利払いの回数を50回から増やせば増やすほど、
複利計算の結果は、
1.19722円に近づいていくことになります。
ぜひ、EXCELを使ってやってみてください。

2006年12月12日　石野　雄一
ご意見ご感想、お待ちしています。

次回パートナーエッセイは、12月14日（木）に、Yoshihara氏が担当します。